4529. Fibonacci numbers: the last digit

Find the last digit of the k-th Fibonacci number.

Fibonacci numbers are defined by the following recurrence relations:

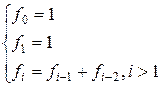
Input. Each line contains a single number k (0 ≤ k ≤ 9223372036854775807).

Output. For each test case print in a separate line the last digit of the k-th Fibonacci number.

Sample input	Sample output
0 1 2 37 135 23	1 1 2 9 7 8

SOLUTION

Fibonacci numbers

Algorithm analysis

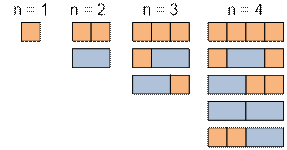
Consider the next problem. In how many ways is it possible to cover the strip 1 × n with domino of size 1 × 2 and squares of size 1 × 1? Let this number of ways be f(n). Obviously that f(1) = 1, f(2) = 2.

If we cover the first cell of the table with a square, then we need to cover the strip 1 × (n – 1), it can be done in f(n – 1) ways. If we cover the first and the second cell of the table with a domino, then we need to cover the strip 1 × (n – 2), it can be done in f(n – 2) ways.

Thus f(n) = f(n – 1) + f(n – 2), so f(n) are Fibonacci numbers.

Let we have a table 1 × (n + m). It can be covered in f(n + m) ways. First we consider the coverings without domino that covers the cells n and n + 1.

Then the first n cells can be covered with squares and dominos in f(n) ways, and the last m cells can be covered with f(m) ways. That is, the entire table can be covered in f(n) * f(m) ways.

Now consider the coverings where one domino covers the cells n and n + 1. We have f(n – 1) * f(m – 1) such coverings.

Summarizing, we get that

f(n + m) = f(n) * f(m) + f(n – 1) * f(m – 1),

f(1) = 1, f(2) = 2.

Let's obtain some identities from the indicated recurrence:

· if m = n, then f(2n) = f(n) * f(n) + f(n – 1) * f(n – 1),

· if m = n + 1, then f(2n + 1) = f(n) * f(n + 1) + f(n – 1) * f(n)

Calculating the Fibonacci numbers using the above relations, we obtain the logarithmic complexity O(log₂n).

Algorithm realization

Since the indices of the calculated Fibonacci numbers have the order of 10¹⁸, it is impossible to use a linear array of this size for memorization. To memorize the results we’ll use the map data structure.

map<long long, long long> fib;

The calculation of the n-th Fibonacci number.

long long f(long long n)

{

if (n <= 1) return 1;

if (n == 2) return 2;

if (fib[n] != 0) return fib[n];

long long k = n / 2;

if (n % 2 == 0)

return fib[n] = (f(k - 1) * f(k - 1) + f(k) * f(k)) % 10;

return fib[n] = (f(k) * (f(k - 1) + f(k + 1))) % 10;

}

The main part of the program. Read the input value n and print the n-th Fibonacci number f(n).

while (scanf("%lld", &n) == 1)

printf("%lld\n", f(n));